Day in and day out, summer after summer when I was a kid, I flew endlessly back and forth over Casco Bay with my father in his Piper Cub seaplane. From the air I saw thousands of spooked seagulls, smooth steel-colored sea rollers in identical ranks, wind-beaten chop, whales, porpoises, surface-churning mackerel, a shark so big it looked like a driveway with fins, the salt-scoured lighthouse at Halfway Rock, weird yellow-orange apparitions of the setting sun, and dark schools of herring snugged up into island coves in the evening.

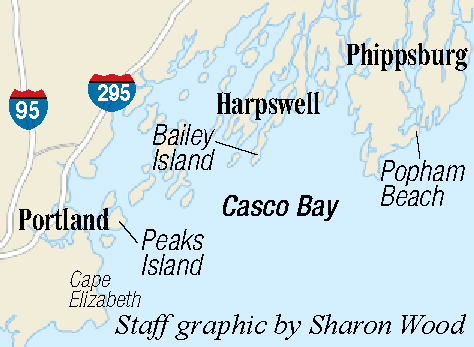
There also was the mysterious fact that most of the islands and rocks were elongated in the same direction, roughly northeasterly. You could see it as we approached Bailey Island to land in Mackerel Cove, a tube of water between two spits of land about the same shape as the cove. Out of the plane and scrambling around on low-tide ledges, you could see grooves and ridges in the rock running in the same direction. A map of Casco Bay looked like clusters of oblongs all parallel to each other.

That grooving, at the small scale and the big scale, happened around 14,000 years ago when a glacier a mile-and-a-half thick was inching back toward the Arctic, scratching ruts and gouging inlets and coves with something like icy claws.

How would you measure the full length of this coved and inletted coast? Would you run your imaginary tape straight from Kittery to Lubec and let it go at that? Or would you measure into the bays too? The detours into Casco, Penobscot, Blue Hill, Frenchman, Machias and Cobscook bays would add uncountable miles — should you measure all the coves? And all their nooks and corners?

It turns out there is literally no end to Maine’s jagged Atlantic contour.

Better mathematical minds than mine were considering this problem of measuring crooked distances before I noticed it at the age of about 10, and one of them — Benoit Mandelbrot — noticed that natural objects such as coastlines do not conform to geometry based on straight lines. In other words, the lines, planes and cubes you learn about in high school geometry are ideal forms that do not actually exist in nature. So how do you measure the irregular thing itself?

Turning out to be a person who notices similarities rather than a person who notices numbers, I don’t understand exactly how Mandelbrot’s methods help figure coastal lengths. But I can explain the general idea. Since a line in nature is not exactly a line, and a plane not a plane, Mandelbrot figured out how to assign a number to the way a line (of a jagged coast, for example) leaks out of its straightness to some extent into a plane. It’s not exactly a plane, but not exactly a line either. If a line is one-dimensional, represented by 1, and a plane is two-dimensional, represented by 2, then the line of Maine’s coast is in between 1- and 2-dimensional. In other words, it is “fractal.”

A study in 2006 calculated the fractal dimensions of four areas of Maine’s coast. The southwest coast, which has a lot of beaches that are more or less straight has a mean fractal dimension of 1.11 — a slight bend off a straight line. The south coast, which includes Casco Bay, is 1.35. (Another analysis showed the fractal dimension of Boothbay, where my mother’s family arrived in the 18th century, is 1.27.) The north coast around Mount Desert Island is 1.23. The northeast coast from Machias into Cobscook Bay is 1.26, although Cobscook has a uniquely irregular coast-scape and comes in at 1.37.

The overall fractal dimension of Maine’s coast looks to be a bit upwards of 1.2.

Now, another thing Mandelbrot noticed about fractal dimensions is that as you look more closely at an irregular line in nature, its shape at large scales tends to be similar to its shape at smaller scales. In other words, along the coast around Casco Bay, the coves have shapes similar to those of the grooves in the ledges, as I noticed when I was a kid. They are described as “self-similar,” which is to say, they are fractals of each other. These similar shapes go on indefinitely downward: The bays are shaped like their coves, the coves are shaped like their ledges, the ledges are shaped like their grooves, the grooves are shaped like their ruts, the ruts are shaped like their scratches.

This apparently is true not only of coastlines, but also of the outline of a snowflake, a mountain range, a mathematically generated pattern. The shape of a portion of an object is basically the same as the overall shape of the object. This goes on infinitely downward as far as there are corners to be turned. And presumably, infinitely upward. A planet-moons system is similar to a star-planets system, and star-planets systems are similar to galaxies.

Nature appears to be fractal through and through, mirroring itself at every turn and nook.

A child is a fractal of an adult. My son at 28 has the same contours I did at his age. And apparently he thinks fractal thoughts. When he was 6, he shone a flashlight on a sheet of shiny brown metal, and the light splayed into a strangely deep-looking cone shape. “Look, Dad,” he said. “It’s a small future.”

The child is father to the man in thought as well as physique, it seems, and no doubt in whatever other form we eventually take. Infinitely upward, it is to be hoped.

Dana Wilde lives in Troy. You can contact him at naturalist1@dwildepress.net. His recent book is “Summer to Fall: Notes and Numina from the Maine Woods,” available from North Country Press. Backyard Naturalist appears the second and fourth Thursdays each month.

Related Stories